快速傅里葉變換(FFT)實現了時域到頻域的轉換,是信號分析中最常用的基本功能之一。FFT變換時,總是從離散數據中選取一部分處理,將其稱為一幀數據。而且FFT是在一定假設下完成的,即認為被處理的信號是周期信號。因此,FFT之前會對這一幀數據進行周期擴展。
以CW信號為例,如果選取的這一幀數據不是信號周期的整數倍,則在周期擴展時會存在樣點的不連續性,如圖1所示。這將導致FFT之后得到的頻譜失真,主要體現在頻率成分上。理論上,頻譜中只包含待測信號的頻率,但實際上此時的頻譜包含眾多的頻率分量。通常將這種現象稱為頻譜泄露效應。
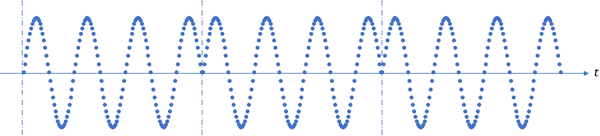
圖1. 周期擴展造成樣點不連續
為了抑制頻譜泄露效應,可以采用諸如Hanning、Kaiser等多種時間窗。還有一種特殊的時間窗——矩形窗,其實就是不加時間窗,直接對原始樣點做FFT變換,上述例子就是采用矩形窗的情況。只有采用矩形窗,而且窗寬度不是信號周期的整數倍時,才會發生明顯的頻譜泄露效應。